Le futur de Bitcoin : signatures de Schnorr

Schnorr est un nom que tous ceux qui suivent l’actualité de Bitcoin ces dernières années ont forcément entendu. Il s’agit d’un algorithme de signature plus simple et plus efficace qu’ECDSA actuellement utilisé.

Pourquoi Satoshi ne l’a-t-il pas implémenté dans ce cas ? La raison en est simplement que Schnorr était protégé par un brevet jusqu’en 2008, et qu’il n’existait donc pas de standard qui aurait permis à Satoshi d’implémenter Schnorr avec autant de sécurité qu’ECDSA(1).

Mais grâce au travail de Peter Wuille et d’Andrew Poelstra, un brouillon de BIP a été proposé en juillet 2018 pour implémenter Schnorr dans Bitcoin. Concrètement, que cela va-t-il changer pour le réseau et ses utilisateurs ?

Et bien de façon surprenante… pas grand-chose en soi. Schnorr produit des signatures environ 10% plus légères qu’ECDSA et est validé légèrement plus vite, mais rien qui ne change la face de Bitcoin à ce stade. Alors pourquoi tant d’excitation à ce sujet ?

Les signatures de Schnorr ouvrent en fait la voie à d’autres améliorations beaucoup plus significatives, et c’est pour ça que vous devriez vous y intéresser dès maintenant.

Aggrégation de clés et multisignatures

En effet, Schnorr a une propriété très intéressante : la linéarité. Un concept mathématique qui signifie qu’on peut additionner les clés publiques et les signatures produites par cet algorithme, et que le résultat sera valide ! Concrètement, cela revient à faire des multisignatures avec n participants, mais une seule clé publique et une seule signature pour la valider.

La killer app de Schnorr est donc la multisignature : tous les signataires additionnent leur clé publique pour en produire une nouvelle totalement impossible à différencier de n’importe quelle autre clé. Les signataires (ou une partie d’entre-eux dans le cas d’une signature de seuil, threshold signature) peuvent ensuite produire collaborativement une signature de taille fixe, elle aussi totalement similaire à n’importe quelle signature de Schnorr, valide avec la clé publique agrégée.

Les bénéfices sont importants :

• Confidentialité/fongibilité : contrairement au fonctionnement actuel des multisignatures, où toutes les clés publiques et toutes les signatures sont publiées dans la timechain au moment de la dépense, avec un multisig Schnorr il est non seulement impossible de savoir combien il y a de signataires et de signatures, mais même qu’il s’agit d’une multisignature !
• Scalabilité : l’espace sur la timechain est cher, les nœuds doivent dépenser de l’énergie pour valider les transactions. En réduisant à une seule le nombre de validations indépendamment du nombre de signataires, Schnorr améliore grandement la scalabilité de Bitcoin.

À noter également que cela éliminerait la principale faiblesse de Lightning en termes de confidentialité, à savoir le fait que les transactions d’ouverture et de fermeture de canaux on-chain sont identifiables. Si les canaux de paiement sont ouverts et fermés avec des multisignatures Schnorr, elles deviennent complètement indiscernables de n’importe quelle autre transaction.

Une implémentation délicate

Très bien, ça a l’air génial et facile, qu’attendons-nous pour l’implémenter ?

Et bien, si vous vous souvenez du début de cet article, il n’existe à l’heure actuelle pas d’autre implémentation de Schnorr que celle de Bitcoin, les éventuels risques sont mal connus et dans un réseau qui sécurise l’équivalent de milliards de dollars et vise l’éternité il s’agit de ne pas se précipiter.

Le problème principal rencontré par Peter Wuille et Andrew Poesltra concerne justement la sécurité des multisignatures. En effet, une implémentation “naïve” de l’aggrégation de clés que nous avons expliquée ci-dessus serait en fait extrêmement dangereuse.

Pour le dire simplement, si les clés peuvent être additionnée entre elles, elles peuvent aussi être soustraites. Cette propriété a des applications intéressantes, mais signifie aussi qu’un participant d’une multisignature pourrait “tricher” en ne donnant pas sa véritable clé publique pour l’aggrégation, mais une clé qui serait le résultat de la sienne moins toutes les autres, ce qui reviendrait à dire qu’il pourrait produire une signature valide avec sa seule, véritable clé privée puisqu’il aurait simplement “annulé” celles de tous les autres signataires !

Cette Rogue Key Attack peut être contrée en demandant à chaque participant de prouver qu’il possède une clé privée correspondante à la clé publique qu’il produit, mais un tel protocole serait très lourd et poserait d’autres problèmes. Avec le Français Yannick Seurin, Poelstra et Wuille ont donc élaboré un protocole de multisignature, Musig, qui à [leur] connaissance, est le premier système de multisignature prouvablement sûr dans le modèle de clés publiques claires (plain public key) qui permet l’aggrégation de clés.

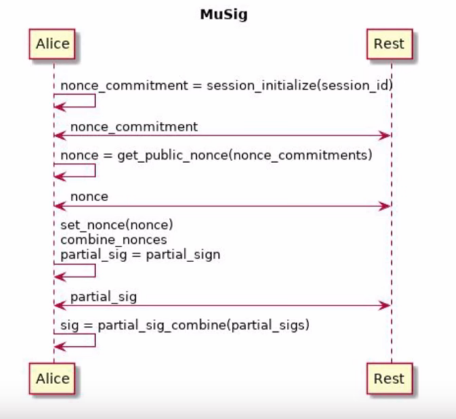
Musig laisse toutefois le problème de l’auditabilité des multisignatures en suspens : dans le cas d’une signature de seuil, par exemple 3-de-5, une signature valide peut être produite par 3 signataires sur 5, mais il est impossible de les identifier a posterio. Cela est évidemment un problème très sérieux dans le cadre d’une organisation, et la solution proposée pour l’instant est d’isoler les différents sous-ensemble de signataires au sein de scripts différents. C’est ce que Taproot, dont je parlerai dans un futur article, cherche à réaliser.

Cross-input aggregation, batch validation

Cette propriété est donc principalement utilisée pour les multisignatures, mais pourrait avoir d’autres applications intéressantes. Une première idée serait d’aggréger toutes les signatures fournies en input d’une transaction pour ne plus avoir à en valider qu’une seule, indépendamment du nombre des inputs. Cela serait révolutionnaire pour des transactions de type CoinJoin par exemple, qui nécessite un grand nombre d’inputs : au lieu d’inscrire sur la timechain et de valider une centaine de signature, il n’y en aurait plus qu’une seule !

Une autre propriété des signatures de Schnorr est la possibilité de les valider en batch : il est possible de prendre un ensemble de n signatures, et de les valider toutes ensemble. Si une ou plusieurs signatures sont invalides, la validation échoue mais on ne peut pas savoir quelle signature est invalide. Ce n’est néanmoins pas un problème dans certains cas d’usage comme la validation de bloc, où le but est de savoir si un bloc est valide ou non : si au moins une signature est invalide, cela suffit à rejeter le bloc et on n’a pas besoin de savoir où se trouve le problème.

Ces améliorations posent néanmoins des difficultés d’implémentation, notamment dans le cadre d’un softfork où les signatures Schnorr et ECDSA doivent coexister, et seront probablement ajoutées dans un second temps.

Plus loin : scriptless scripts, Taproot

Au-delà de cette capacité d’aggrégation et les possibilités que nous venons d’évoquer, Schnorr permet d’envisager d’autres façons intéressantes de construire des transactions.

Tout d’abord, il y a les scriptless scripts, c’est-à-dire des smart contracts qui ne font pas appel à un script, mais utilise la cryptographie pour autoriser ou interdire certaines actions. En fait, la multisignature de Schnorr que nous venons de détailler en est déjà un exemple : au lieu de lister les clés publiques des signataires et d’écrire un script qui ne validera la transaction que si un nombre n-de-m de signatures valides est fournie, on utilise les propriétés cryptographiques des signatures pour arriver au même résultat.

Une autre application très intéressante du même principe est l’adaptor signature, qui consiste à créer une signature à laquelle on a soustrait une valeur arbitraire secrète. Cette signature “mutilée” peut être partagée avec quelqu’un d’autre, et le secret sera révélé lorsque je fournirai une autre signature. À part les parties du contrat, personne ne peut savoir que ces deux signatures sont liées, ni découvrir le secret.

Cette construction permet de réaliser par exemple des atomic swap, c’est-à-dire des échanges de bitcoins sans intermédiaire et sans confiance, mais on peut espérer d’autres mécanismes ingénieux qui permettront de réduire encore la nécessité d’exécuter des scripts pour valider des transactions, ce qui n’est pas vraiment là où une timechain publique comme Bitcoin peut briller.

Schnorr et ses propriétés de linéarité permettent en effet d’envisager de verrouiller des fonds au moyen de scripts (qui ne sont au fond que des smarts contracts) beaucoup plus complexes qu’aujourd’hui, et c’est l’objet des propositions de Greg Maxwell Taproot et Graftroot, qui seront le sujet de mon prochain article.

(1)outre l’implémentation réalisée pour bitcoin, il en existe une autre dans la librairie cryptographique NaCl (“Salt”)

Pour aller plus loin :

1. Présentation des signatures de Schnorr par Yannick Seurin au séminaire Cryptofinance organisé par Cyril Grunspan et Ricardo Marco-Pérez
2. Les publications de Y. Seurin sur son site
3. La présentation de Schnorr (et Taproot/Graftroot) par Peter Wuille au SF Bitcoin Dev Meetup
4. La présentation de Peter Wuille à Stanford sur les bénéfices et les défis de Schnorr
5. Le #3 de la newsletter mail de Bitcoin Optech, une ressource de grande valeur pour se tenir au courant de l’actualité technique de Bitcoin
6. L’article Musig par G. Maxwell, A. Poelstra, Y. Seurin et P. Wuille
7. Le brouillon de BIP Schnorr